Studying Software

Team

Kim de Groot, Anne Helmond, Shirley Niemans, Warren Sack, Marijn de Vries Hoogerwerff

Geographical Issue Distance

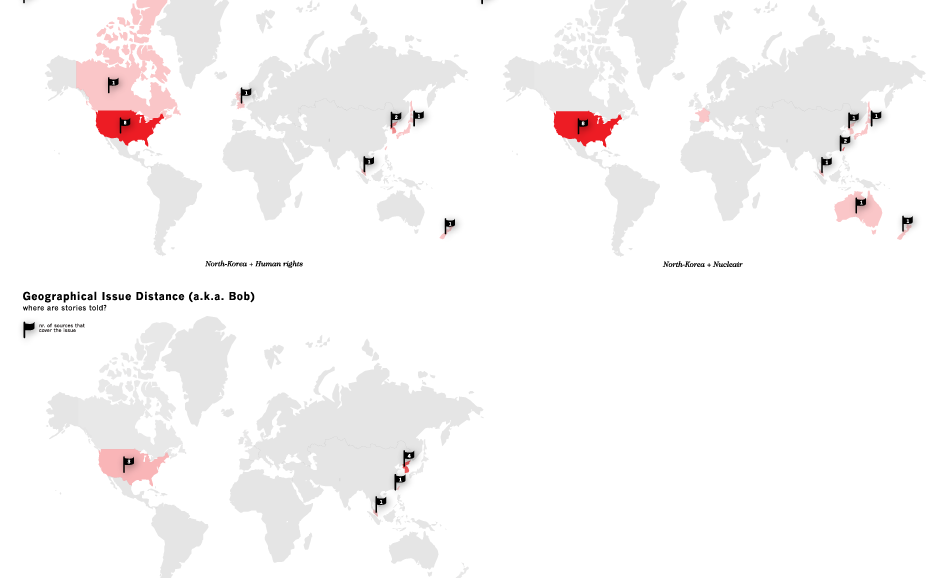
We define a process for using Google News to explore whether, for any given issue, geographical distance distinguishes significant differences of opinion. For instance, when discussing the issue of the Iraq War, is there a significant difference between French opinions and American opinions? Or, given the issue of "whaling" does the Northern Hemisphere -- e.g., Norway, Japan, etc. -- have a significantly different way of describing the issue than does the Southern Hemisphere?

Question

Does geographical distance distinguish significant differences of opinion about a given issue?

Method

We start by making a set of simplifying assumptions so that a prototype can be built quickly. We will revisit these assumptions later, once we have built the prototype and determined what might be gained by not simplifying.

(i) First, we make the assumption that this sort of analysis can be done using one language, English. Thus, we assume that measuring the difference between French and American opinion is still possible if we limit our analysis to the English-language newspapers of France. This simplification, of monolinguism, permits us to query Google News using only English-language terms rather than translating each of our queries.

(ii) Second, we use a simplified model of geography whereby each news source is identified with a country, rather than, for example, a city of even latitude and longitude. This assumption requires further simplifications: (a) we assume that countries have a continguous geography, thus we need to ignore the fact that between Alaska and the continental U.S. lies the country of Canada; and, (b) we assume a normalized distance between countries that is tantamount to computing path length of a graph in which each node in the graph is a country; and, each link in the graph denotes geographical adjacency of two countries; each link is of unit 1. So, the distance from the U.S. to Canada is 1; the distance from the U.S. to Mexico is also 1. The distance from the U.S. to Guatamala and Belize is 2 (because one must traverse Mexico to get to them from the U.S.); the distance from the U.S. to Honduras is 3; etc.

Input and Output: Given these simplifications we can define a process where the input is a query (of one or more search terms) and the output is a set of colored, geographical maps. Each of the maps produced by the process represents the distribution of co-occurence between the query term(s) and a second noun or noun phrase that also appears with the query term(s). For instance, if the query is "North Korea" the process -- to be defined below -- might determine that "North Korea" frequently co-occurs with the noun "reunification" in the news sources of North Korea, South Korea, Japan, and China; co-occurs infrequently in Brazil; and, co-occurs not at all in the rest of the world. Then, the colored map might show most of Asia tinted orange with 100% opacity; Brazil tinted orange with 20% opacity; and the rest of the world left blank.

Protocol

Here, then, is a more detailed description of the process to be implemented:

(1) Accept a set of one or more terms as a search query, Q.

(2) Submit Q to Google News.

(3) Store the set of results from Google News as a list of URLs, R.

(4) For each r of R, determine the location of r and store it in a hash, L{r}. Each location is a country. The location of each site can be determined by using, for example, the information on this site -- http://www.ipl.org/div/news/ -- along with a database of city-to-country pairs and some calls to the whois service to determine where unknown URLs are registered.

(5) For each r of R, extract the other nouns and noun phrases that occur on the same document (located at the given URL), using the OpenCalais tool. Actually, here a further simplifying assumption will be made. Rather than fetch the entire document represented by the URL, r, one can use the summary of the document found next to each URL returned by Google News. Either way (with or without the simplifying assumption), let us call these "co-terms," the nouns and noun phrases that co-occur with the query, Q. Thus, for each r of R, there is a list of co-terms, which we will denote as T{r}.

(6) Recaste the lists of T into normalized, weighted vectors where each position in the vector represents a co-term and each weight represents the number of times the co-term was found in the document r divided by the total number of co-terms in the document; these weighted vectors will be called V and a given document's co-terms will be denoted V{r}.

(7) For each v of V, calculate the distance between all of the other vectors of V. Presumably many of the documents of R will be unlike in length. So, pick a measure of distance, like cosine(v1-v2), which is not sensitive to differences of document length. I.e., pick a measure in which it makes sense to measure the distance between a short document and a long document; or, in this case, between a vector, v1, that contains many weights and another vector, v2, that contains many more or many fewer weights. The resulting distance matrix will be named D and D{r1,r2} will denote the distance between two documents, r1 and r2.

(8) Calculate a second distance matrix, G, such that G{r1,r2} is a measure of the simplified geographical distance between the country location of r1 and the country location of r2. This is tantamount to a path length analysis on the graph described above in assumption (ii).

(9) Given an integer k -- perhaps chosen by the user or perhaps preset as 2, 3 or 4 -- and a cluster algorithm, such as K-means, cluster the elements of R into k partitions using the distances recorded in D. Return a hash C, such that for each 1 <= i <= k, C{i} returns a list that contains all of the elements URLs in cluster i.

(10) For 1 <= i <= k, find centerOfMass(C{i}) using V

(11) For 1 <= i <= k, find the mean squared error of G{ri,centerOfMass(C{i})} - G{ri,centerOfMass(C{j})} for all 1 <= j <= k; store as MSE{i}; Note that with the simplified geographical distance -- i.e., the distance as defined in assumption (ii) above -- the distances will all be integers.

(12) Construct maps: For 1 <= i <= k , construct a map M{i} such that foreach member of C{i} is marked according to its position on the map.

(13) Sort the list of maps M, such that if MSE{i} < MSE{j}, M{i} is ranked before M{j}

(14) Output the list of sorted maps.

Maps (demo)